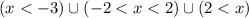Question

2(x+3)^3(x+2)^3(x-2)^2>0

Answer 1

First observe that the left hand side evaluates to 0 whenever
`x=-3`,
`x=-2`, or
`x=2`.

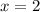
So let's take numbers to either side of these roots. If
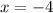
`x=-4`, for instance, we have
`(-4+3)^3=(-1)^3=-1<0`,
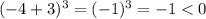
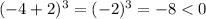
`(-4+2)^3=(-2)^3=-8<0`, and
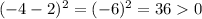
`(-4-2)^2=(-6)^2=36>0`. We would be multiplying a positive number (2) by two negatives (-1 and -8) and a positive (36), which gives a positive number. So, we know
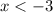
`x<-3` must be a solution set.

Doing the same for numbers between/beyond the other three cases,
`-3<x<-2`,
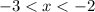
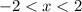
`-2<x<2`, and
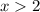
`x>2`, we would get, respectively, a negative, positive, and a positive.

The entire solution set would then be the union of the intervals over which we get a positive number, i.e.
`(x<-3)\cup(-2<x<2)\cup(2<x)`