Question

Find the zeros (roots) of the following equations.

f(x) = 2x5 - 9x4 + 12x3 - 12x2 + 10x - 3 = 0

Answer 1

Hello,

f(1)=2-9+12-12+10-3=0 ===>(x-1)*....
f(3)=2*3^5-9*3^4+12*3^3-12*3^2+10*3-3=0 ===> (x-3)*....
f(1/2)=2*(1/2)^5-9*(1/2)^4+12*(1/2)^3-12*(1/2)^2+10*1/2-3=0 ===>(2x-1)*...

f(x)=(x-1)(x-3)*(2x-1)*(x²+1)
In C, x=i ou x=-i

Zeros are 1/2,1,3,i,-i

Answer 2

Therefore the roots of equation 1 are 1,3 1/2,-i,+i

Explanation:

in this question we have given

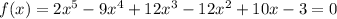`f(x) = 2x^5 - 9x^4 + 12x^3 - 12x^2 + 10x - 3 = 0`.......1

we have to find the roots of this equation

put x=1 in equation 1

`f(1)=2-9+12-12+10-3\\f(1)=0`

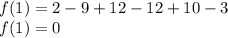
It means x=1 is root of equation 1

now put x=3 in equation 1

`f(3)=2*3^5-9*3^4+12*3^3-12*3^2+10*3-3\\f(3)=0`

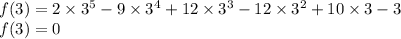
therefore,x=3 is root of equation 1

Now put x=
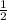`(1)/(2)` in equation 1

`f((1)/(2))=2* ((1)/(2) )^5-9*((1)/(2))^4+12*((1)/(2))^3-12*((1)/(2))^2+10* (1)/(2)-3\\f((1)/(2))=0`

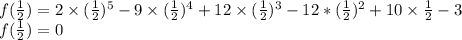
It means x=
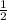`(1)/(2)` is also root of equation 1

therefore equation one can be written as

`f(x)=(x-1)(x-3)(2x-1)(x^2+1)`

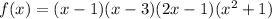
therefore remaining 2 roots can be calculated by solving

`x^2+1=0\\x=\sqrt(-1)\\x=i,-i`

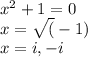
Therefore the roots of equation 1 are 1,3 1/2,-i,+i