Question

A ball is thrown vertically upward from the top of a 200 foot tower, with an initial velocity of 5 ft/sec. Its position function is s(t) = –16t2 + 5t + 200. What is its velocity in ft/sec when t = 3 seconds?

Answer 1

v = ds/dt = -32t + 5

at t = 3 velocity = -96 + 5 = -91 ft/sec answer

Answer 2

The velocity would be - 91 ft/sec.

Explanation:

Given,

The function that shows the position of the ball after t seconds,

`s(t) = -16t^2 + 5t + 200`

Since, velocity is the changes in position with respect to time,

That is, if v(t) is the velocity of the ball after t second,

`\implies v(t)=(d)/(dt)(s(t))`

`=(d)/(dt)(-16t^2 + 5t + 200)`

`=-32t+5`

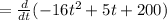
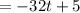
Hence, the velocity after 3 seconds is,

`v(3)=-32(3)+5=-96+5=-91\text{ ft per seconds}`