Question

There are currently 21 frogs in a (large) pond. The frog population grows exponentially, tripling every 7 days. How long will it take (in days) for there to be 150 frogs in the pond?

Answer 1

Let x = number of days

The initial number of frogs = 21.
The number of frogs triples every 7 days.
The exponential function that models the number of frogs with respect to the number of days is

`y = 21(3^(x/7) )`

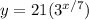
When the population is 150, then

`21(3^(x/7)) = 150 \\\\ 3^(x/7) = 150/21 \\\\ (x)/(7) ln(3) = ln(150/7) \\\\ x = 7( (ln(150/21))/(ln(3)) ) = 12.527`
A graph of y versus confirms the answer.

Answer: 12.5 days