check the picture below.
![\bf \begin{array}{lllll} &x_1&y_1&x_2&y_2\\ % (a,b) &({{ -2}}\quad ,&{{ 5}})\quad % (c,d) &({{ -1}}\quad ,&{{ 1}}) \end{array} \\\\\\ % slope = m slope = {{ m}}= \cfrac{rise}{run} \implies \cfrac{{{ y_2}}-{{ y_1}}}{{{ x_2}}-{{ x_1}}}\implies \cfrac{1-5}{-1-(-2)}\implies \cfrac{1-5}{-1+2} \\\\\\ \cfrac{-4}{1}\impliedby\stackrel{slope~of}{PQ}]()
![\bf \begin{array}{lllll} &x_1&y_1&x_2&y_2\\ % (a,b) &({{ -1}}\quad ,&{{ 1}})\quad % (c,d) &({{ 7}}\quad ,&{{ 3}}) \end{array} \\\\\\ % slope = m slope = {{ m}}= \cfrac{rise}{run} \implies \cfrac{{{ y_2}}-{{ y_1}}}{{{ x_2}}-{{ x_1}}}\implies \cfrac{3-1}{7-(-1)}\implies \cfrac{3-1}{7+1} \\\\\\ \cfrac{2}{8}\implies \cfrac{1}{4}\impliedby \stackrel{slope~of}{QR}]()
now, two lines who meet at a perpendicular angle, have a
negative reciprocal slope of each other, to make it short, if you multiply their slopes, you should get -1 as the product, if they're indeed perpendicular.
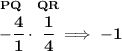
low and behold, they're indeed perpendicular, thus that angle is indeed a right-angle.