To answer this question, we need to make use of the cumulative standard normal distribution. No matter what the probability we are finding for. The cumulative normal distribution will give us a z-score (the value in standard deviations the raw value, x, is from the mean).
Then, we have that the z-score is given by:
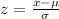
We have that the cumulative standard normal distribution gives us value for values less than a z-score. Then, we need to find this z-score using the cumulative standard distribution as follows:
![P(xThen, finding the value that corresponds to this probability in a cumulative standard distribution using a table, we have that z = 2.2.<p>Therefore:</p>[tex]P(z<2.2)=0.9861]()
Or

In summary, the value for z is equal to z = 2.2.