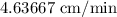Solution:
The area of a triangle is expressed as
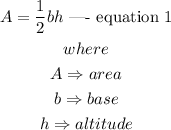
From equation 1, taking the derivative of A with respect to t, we have
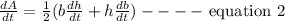
Given that the altitude is increasing at a rate of 2.5 cm/minute while the area is increasing at a rate of 5 square cm /minute, this implies that
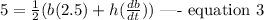
To evaluate the rate at which the base is changing when the altitude is 8.5 cm and the area is 84 square cm, we have
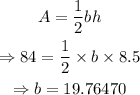
By substitution, we have
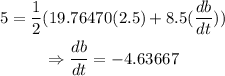
Hence, the base changes at