Answer:
Option C is correct.
Explanation:
The formula is =
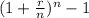
r = rate of interest
n = number of times its compounded
1. 4.0784% compounded monthly
here n = 12
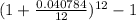 = 1.0403-1 = 0.0403
= 1.0403-1 = 0.0403
2. 4.0798% compounded semiannually
here n = 2
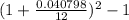 = 1.0066-1 = 0.0066
= 1.0066-1 = 0.0066
3. 4.0730% compounded daily
here n = 365
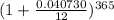 = 3.328-1 = 2.328
= 3.328-1 = 2.328