Note that the angle whose measure is
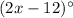
is an exterior angle.
Thus, the sum of the measures of this exterior angle, and the 2 opposing interior angles is not 180°.
It is the sum of the measure of its supplementary angle, and the other 2 opposing interior angles, which is equal to 180°.
So first, we find the measure of the supplementary angle (which is the third interior angle):
180°-(2x-12)°=180°-(2x)°+12°=192°-(2x)°.
Second, the sum of the measures of the interior angles is 180°, so:
192°-(2x)°+30°+x°=180°
192°-180°+30°=(2x)°-x°
42°=x°
So, x=42.
The measure of the exterior angle is thus:
(2x-12)°=(2*42-12)°=(84-12)°=72°
Answer: 72°