Question

A consumer group claims that the mean annual consumption of high fructose corn syrup by a person in the U.S. is 48.8 pounds. A random sample of 120 people in the U.S. has a sample mean annual consumption of high fructose corn syrup of 49.5 pounds. Assume the population standard deviation is 3.6 pounds. evidence to support the group’s claim? 1). State the hypothesis: H0 : Ha : 2). Specify the level of significance   3). Sketch the sampling distribution 4). Calculate the test statistic At = 0.05, is there enough 5). Find the P-value and shade this in the distribution in (3): 6). Decision (using the P-value): 7). Write a statement to interpret the decision in the context of the original claim 2

Answer 1

Part 1:

The null hypothesis (H0) represents the claim to be tested while the alternative hypothesis (Ha) is the opposite of the claim.

Given that a consumer group claims that the mean annual consumption of high fructose corn syrup by a person in the U.S. is 48.8 pounds.

The null and alternative hypothesis are:


`H_0:\mu=48.8 \\ \\ H_a:\mu\\eq48.8`



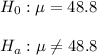
Part 2:

From the question, we are testing the hypothesis at a level of significance
`(\alpha=0.05`



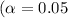
Part 3:

Because the sample size is big enough (i.e 120), we can assume that the distribution is normally distributted.

Recall that the central limit theorem states that given a sufficiently large sample size from a population with a finite level of variance, the mean of all samples from the same population will be approximately equal to the mean of the population all of the samples will follow an approximate normal distribution pattern.
The shape of a nomal distribution curve is attached.



Part 4:

The test statistics is calculated as follows:


`z= (X-\mu)/( (\sigma)/(√(n)) )\\ \\= (48.8-49.5)/((3.6)/(√(120)))\\ \\ = (-0.7)/((3.6)/(10.95)) = (-0.7)/(0.3286)\\ \\ =\bold{-2.13}`



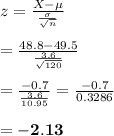
Part 5:

The P-value is obtained as follows:


`P(-2.13)=0.01659`

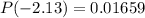
Since the test is a two tailed test, the P-value for the test is given by

2(0.01659) = 0.03318



Part 6:

Since, the P-value is 0.033 and is less than the level of significance 0.05, we reject the null hypothesis.


Part 7:

We conclude that there is enough evidence to reject the consumer group's claim that the mean annual consumption of high fructose corn syrup by a person in United Sates is 48.8 pounds at the level of significance α = 0.05.