Question

For what values of b does the value of the fraction 5−2b /4 belong to the interval [−2; 1]?

Answer 1

Answer: The required value of b lies in the interval [0.5, 6.5].

Step-by-step explanation: We are given to find the value of b so that the following fraction belong to the interval [−2, 1] :

`f=(5-2b)/(4).`

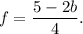
According to the given information, we can write

`-2\leq f\leq 1\\\\\Rightarrow -2\leq (5-2b)/(4)\leq1\\\\\Rightarrow -8\leq 5-2b\leq 4\\\\\Rightarrow -8-5\leq-2b\leq 4-5\\\\\Rightarrow -13\leq -2b\leq -1\\\\\Rightarrow 13\geq 2b\geq 1\\\\\Rightarrow (13)/(2)\geq b\geq (1)/(2)\\\\\Rightarrow 6.5\geq b\geq 0.50`

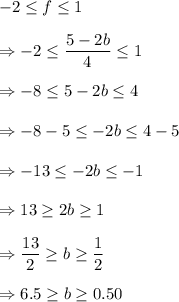
Thus, the required value of b lies in the interval [0.5, 6.5].

Answer 2

The easiest way to solve this is as an inequality. Here's what it's saying we have:

`-2 \leq {(5-2b)/(4)}\leq1`

First, multiply everything by 4 to clear the denominator:

`-8\leq5-2b\leq4`

Subtract 5 from both sides:

`-13\leq-2b\leq-1`

In the last step, we need to divide everything by -2 which will flip both inequality signs, so we have:

`(13)/(2)\geq b \geq (1)/(2)`

So b is in the interval
`[(1)/(2),(13)/(2)]`.