Answer:
A.
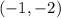
D.
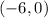
E.
Explanation:
We have been given an inequality
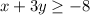 . We are asked to find the ordered pairs that are solution to the given inequality.
. We are asked to find the ordered pairs that are solution to the given inequality.
Let us check each ordered pair by substituting in the given inequality.
A.
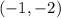

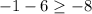
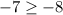
Since the given inequality holds true, therefore, ordered pair
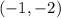 is a solution for the inequality.
is a solution for the inequality.
B.
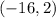
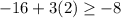
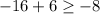

Since the given inequality is not true, therefore, ordered pair
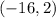 is not solution for the inequality.
is not solution for the inequality.
C.
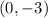
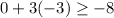
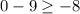
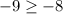
Since the given inequality is not true, therefore, ordered pair
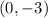 is not solution for the inequality.
is not solution for the inequality.
D.
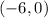
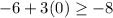

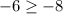
Since the given inequality holds true, therefore, ordered pair
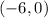 is a solution for the inequality.
is a solution for the inequality.
E.
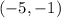
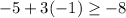
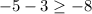
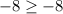
Since the given inequality holds true, therefore, ordered pair
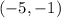 is a solution for the inequality.
is a solution for the inequality.