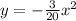Question

Write an equation of the parabola with focus (0, −5/3) and directrix y=5/3

I know the formula is y= 1/4p x^2 but i am having trouble with the fractions being implemented.
p=-5/3

Answer 1

Given:
The focus is at (0, -5/3)
The directrix is y = 5/3

A standard form of the equation for a parabola is
y = a(x- h)² + k
with the focus at (h , k + 1/(4a)),
and the directrix at y = k - 1/(4a)

Therefore
h = 0 (1)
k + 1/(4a) = -5/3 (2)
k - 1/(4a) = 5/3 (3)

Add (2) and (3).
2k = 0
k = 0

Therefore the vertex is at (0,0).
From (2), obtain
1/(4a) = -5/3
4a = -3/5
a = -3/20

The equation of the parabola is
y = -(3/20)x²

The graph is shown below.

Answer:
`y=- (3)/(20) x^(2)`