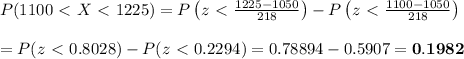The probability that a randomly sample of a normally distributed data with a mean, μ, and standard deviation, σ, is between two numbers (a, b) is given by:
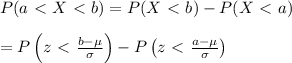
Given that the
september energy consumption levels for single-family homes are found to be normally distributed with a mean of 1050 kwh and a standard deviation of 218 kwh.
The probability that the september energy consumption level of a randomly selected home is between 1100 kwh and 1225 kwh is given by: