Question

JIMMMM! :)

Part A: Explain why the x-coordinates of the points where the graphs of the equations y = 2^x and y = 4^x−2 intersect are the solutions of the equation 2^x = 4^x−2. (4 points)

Part B: Make tables to find the solution to 2^x = 4^x−2. Take the integer values of x between −4 and 4. (4 points)

Part C: How can you solve the equation 2^x = 4^x−2 graphically? (2 points)

Answer 1

Hello there!

Part A: The point or points of intersection are the values of the variables which satisfy both equations at a particular point.

If
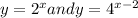
`y=2^x and y=4 ^(x-2)` and the solution of which will satisfy both equations. This idea of equating the two equations is something that you would have come across before, maybe without realizing it.
Consider this:

`x^2 + 6x + 9=0 This can also be looked at as being the two equations: y=x^2 +6x+9 and y=0`
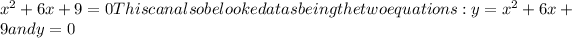
So the points of intersection are the roots in this case and satisfy the equation:



Part B:
You just put integer values between -4 and 4 in each equation and when the output is the same for both that is the solution.


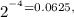
`2^ ^(-4) = 0.0625 ,` and
`4 ^(-6) = 0.000244`

`2 ^(-3) = 0.125,`
`4 ^(-5) =0.000977`

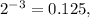
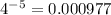
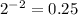
`2 ^(-2) =0.25` and
`4 ^(-4) =0.003906`

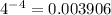
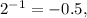
`2 ^(-1)= -0.5,` and
`4 ^(-3) =0.01563`

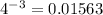
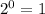
`2^0 =1` , and
`4 ^(-2) =0.0625`

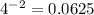
`2^1 = 2` and
`4 ^(-1) =0.25`

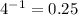
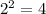
`2^2 =4` and
`4^0 =1`

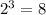
`2^3 =8` and
`4^1=4`

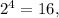
`2^4 =16,` and
`4^2 = 16` (This is the solution when x=4)


Part C:
To solve graphically you just plot the two equations
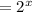
`=2^x` and
`y=4 ^(x-2)`
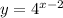
Together graph of
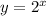
`y=2^x` and
`y=4 ^(x-2)`

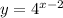
The picture below is how the graph looks like.
Full Credit to my online calculator 'cause we don't have a graphing calculator here.

I hope I helped!

Answer 2

Part A

The x coordinates are the inputs of the functions f(x) = 2^x and g(x) = 4^(x-2)

If we have some input x that leads to f(x) = g(x), then this x value is a solution. It makes the equation f(x) = g(x) true. This is why the x coordinate of the intersection point of y = 2^x and y = 4^(x-2) is the solution.

-------------------------------------------------------------------------
Part B

See attached for the table. See figure 1.

This is how you get the results you see in the table
Plug x = -4 into f(x) to get:
f(x) = 2^x
f(-4) = 2^(-4)
f(-4) = 0.0625

Do the same for g(x):
g(x) = 4^(x-2)
g(-4) = 4^(-4-2)
g(-4) = 4^(-6)
g(-4) = 0.000244140625

-------------------
Plug x = -3 into f(x) to get:
f(x) = 2^x
f(-3) = 2^(-3)
f(-3) = 0.125

Do the same for g(x):
g(x) = 4^(x-2)
g(-3) = 4^(-3-2)
g(-3) = 4^(-5)
g(-3) = 0.0009765625

-------------------
Plug x = -2 into f(x) to get:
f(x) = 2^x
f(-2) = 2^(-2)
f(-2) = 0.25

Do the same for g(x):
g(x) = 4^(x-2)
g(-2) = 4^(-2-2)
g(-2) = 4^(-4)
g(-2) = 0.00390625

-------------------
Plug x = -1 into f(x) to get:
f(x) = 2^x
f(-1) = 2^(-1)
f(-1) = 0.5

Do the same for g(x):
g(x) = 4^(x-2)
g(-1) = 4^(-1-2)
g(-1) = 4^(-3)
g(-1) = 0.015625

-------------------
Plug x = 0 into f(x) to get:
f(x) = 2^x
f(0) = 2^(0)
f(0) = 1

Do the same for g(x):
g(x) = 4^(x-2)
g(0) = 4^(0-2)
g(0) = 4^(-2)
g(0) = 0.0625

-------------------
Plug x = 1 into f(x) to get:
f(x) = 2^x
f(1) = 2^(1)
f(1) = 2

Do the same for g(x):
g(x) = 4^(x-2)
g(1) = 4^(1-2)
g(1) = 4^(-1)
g(1) = 0.25

-------------------
Plug x = 2 into f(x) to get:
f(x) = 2^x
f(2) = 2^(2)
f(2) = 4

Do the same for g(x):
g(x) = 4^(x-2)
g(2) = 4^(2-2)
g(2) = 4^(0)
g(2) = 1

-------------------
Plug x = 3 into f(x) to get:
f(x) = 2^x
f(3) = 2^(3)
f(3) = 8

Do the same for g(x):
g(x) = 4^(x-2)
g(3) = 4^(3-2)
g(3) = 4^(1)
g(3) = 4

-------------------
Plug x = 4 into f(x) to get:
f(x) = 2^x
f(4) = 2^(4)
f(4) = 16

Do the same for g(x):
g(x) = 4^(x-2)
g(4) = 4^(4-2)
g(4) = 4^(2)
g(4) = 16

Note that since the input x = 4 leads to the same output (16) this makes x = 4 a solution.

-------------------------------------------------------------------------
Part C

To solve graphically, you need to use the table in part B to draw a curve through the set of points. Then determine where the curves cross (if they cross at all). You may need to adjust the graph window if the intersection point is off the screen.

See figure 2 for the graph (attached as well). Point A in green is the intersection point.
A = (4,16)
so x = 4 is the solution to f(x) = g(x).