Question

If f(x)=square root of 2-x and g(x)=x-1, then find the domain of h(x)=f(x)/g(x)

Answer 1

Let's examine what the conditions on the domains of f and g have to be before we examine h. Since f is defined:


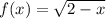
`f(x)= √(2-x)`, we know that the function will be undefined when 2 - x < 0, or when x > 2, so we have the restriction on our domain that x ≥ 0.

g(x) has no such restrictions and is defined for all possible values of x, so its domain is all real numbers, or
`\mathbb{R}`.

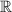
Since h(x) is a rational function, we know that it's undefined when its denominator is 0. In this case, our denominator is g(x), so the function is undefined when g(x)=0. x - 1 = 0 only when x = 1, so the second restriction on our domain for h is that x ≠ 1. Putting those two together, we find that the domain of h(x) is all values of x ≥ 0, where x ≠ 1.

Answer 2

Domain of h(x) : [2,∞)

Explanation:

Given: Two functions

`f(x)=√(2-x)`

`g(x)=x-1`

Composite function,
`h(x)=(f(x))/(g(x))`

`f(x)=√(2-x)`, It is square root function. As we know square root function is always greater than 0.

2-x ≥ 0

2 ≥ x

Domain of f(x) : [2,∞)

`g(x)=x-1`, It is straight line equation (Linear function) As we know domain of linear function is all real number.

Domain of g(x) : (-∞,∞)

`h(x)=(f(x))/(g(x))`

`h(x)=(√(2-x))/(x-1)` , It is rational function. Denominator can't be zero.

So, x-1 ≠ 0

x ≠ 1

Now, we will see domain of h(x) common all three domain.

Domain of h(x): [2,∞)

Hence, The domain of h(x) is [2,∞)