The range is all the possible y-values.
For a parabola that opens up, it is everything greater than the vertex.
If the vertex is (h,k) then the range is y >= k.
Vertex can be found using completing the square:
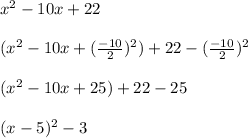
(h,k) = (5,-3) ------> Range is y >= -3
Vertex may also be found using formula
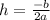
a = 1, b = -10, c = 22
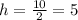
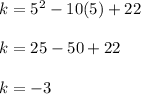
------> Range is y >= -3