To solve a system of equation by elimination we first write each of the equation of the system in standard form. In this case the system is already written in this form:

Now we need to choose one of the variable to have opposite coefficients, that is, to have the same absolute value but different sign.
For example, if we multiply the first equation by 2 the coefficient of x would be 12 in the first equation and -12 in the second equation; with this we achieve the opposite coefficients condition we wanted, let's see this:
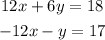
To determine for which value we need to multiply one of the equation we need to look at the original system and determine for which one we would achieve the opposite coefficient condition stated above.
Now that we have opposite coefficients for one of the variables we add the equations:
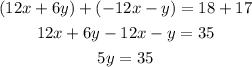
Notice how once we add the equations the variable with opposite coefficients cancel out, this is the what we mean by "elimination" in the method, we are eliminating one variable to get an equation with just one variable that we can solve. Let's solve the equation for y:

Now that we have the value for one of the variables we plug it in one of the original equations to get an equation for the other variable. Let's plug the value of y in the first equation and solve the resulting equation for x:
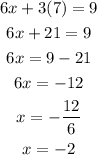
Therefore we conclude that the solution of the system is x=-2 and y=7