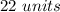Question

What is the perimeter of a polygon with vertices at

(−1, 3) , ​ (−1, 6) ​, (2, 10) , ​ (5, 6) ​​, and ​​ ​ (5, 3) ​?

Enter your answer in the box. Do not round any side lengths.​

Answer 1

(-6,6) to (2,10) and (2,10) to (5,6) = square root of 3 squared plus 4 squared = 5 3 plus 5 plus 5 plus 3 plus 6 = 22

Answer 2

we know that

the perimeter of a polygon is the sum of the length sides

in this problem we have five vertices

so

the polygon has five sides

Let

`A(-1,3)\\B(-1,6)\\C(2,10)\\D(5,6)\\E(5,3)`

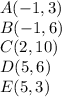
the perimeter is equal to

`P=AB+BC+CD+DE+AE`

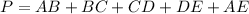
The formula to calculate the distance between two points is equal to

`d=\sqrt{(y2-y1)^(2)+(x2-x1)^(2)}`

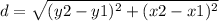
Step 1

Find the distance AB

`A(-1,3)\\B(-1,6)`

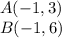
substitute the values in the formula

`d=\sqrt{(6-3)^(2)+(-1+1)^(2)}`

`d=\sqrt{(3)^(2)+(0)^(2)}`

`dAB=3\ units`

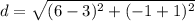
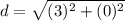
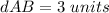
Step 2

Find the distance BC

`B(-1,6)\\C(2,10)`

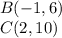
substitute the values in the formula

`d=\sqrt{(10-6)^(2)+(2+1)^(2)}`

`d=\sqrt{(4)^(2)+(3)^(2)}`

`dBC=5\ units`

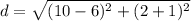
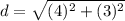
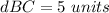
Step 3

Find the distance CD

`C(2,10)\\D(5,6)`

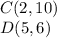
substitute the values in the formula

`d=\sqrt{(6-10)^(2)+(5-2)^(2)}`

`d=\sqrt{(-4)^(2)+(3)^(2)}`

`dCD=5\ units`

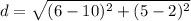
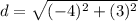
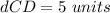
Step 4

Find the distance DE

`D(5,6)\\E(5,3)`

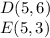
substitute the values in the formula

`d=\sqrt{(3-6)^(2)+(5-5)^(2)}`

`d=\sqrt{(-3)^(2)+(0)^(2)}`

`dDE=3\ units`

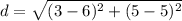
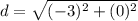
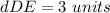
Step 5

Find the distance AE

`A(-1,3)\\E(5,3)`

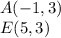
substitute the values in the formula

`d=\sqrt{(3-3)^(2)+(5+1)^(2)}`

`d=\sqrt{(0)^(2)+(6)^(2)}`

`dAE=6\ units`

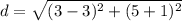
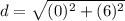
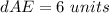
Step 6

Find the perimeter

the perimeter is equal to

`P=AB+BC+CD+DE+AE`

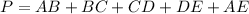
substitute the values

`P=3+5+5+3+6=22\ units`

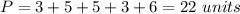
therefore

the answer is

the perimeter of the polygon is
`22\ units`