a)
In order to calculate the area to the left of 25, first let's find the z-value using the formula below:
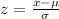
Where x = 25, the mean is equal to 23 and the standard variation is equal to 4.
So we have:
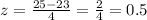
Looking at the z-table for the probability of z <= 0.5, we have 0.6915, so the area to the left of 25 is equal to 0.6915.