Question

Are two lines parallel, perpendicular, or neither3x+7y=157x-3y=6

Answer 1

We can check if two lines are either parallel or perpendicular if we apply the following rule:

If two lines are parallel, then

`\begin{gathered} \text{The slope of the two lines must be equal} \\ m_1=m_2 \end{gathered}`

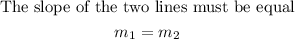
If two lines are perpendicular, then

`\begin{gathered} \text{The two slopes will be related by} \\ m_1m_2=-1 \end{gathered}`

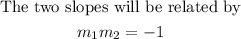
So to check if the two lines are parallel

Step 1: Write the equation of a line in slope-intercept form

y=mx+c

Step2: Find the slopes of the equation

For the first line

`\begin{gathered} 3x+7y=15 \\ 7y=-3x+15 \\ y=-(3)/(7)x+(15)/(7) \end{gathered}`

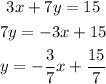
So, the slope of the first line when compared to the general equation

`m_1=-(3)/(7)`

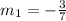
For the second line

`\begin{gathered} 7x-3y=6 \\ 3y=7x-6 \\ y=(7)/(3)x-(6)/(3) \\ y=(7)/(3)x-2 \end{gathered}`

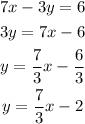
So, the slope of the second line when compared to the general equation

`m_2=(7)/(3)`

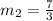
The next step is to use the rule to confirm

Since

`\begin{gathered} m_1=-(3)/(7) \\ m_2=(7)/(3) \\ \\ m_{1\text{ }}* m_{2\text{ }}=-(3)/(7)*(7)/(3)=-1 \end{gathered}`

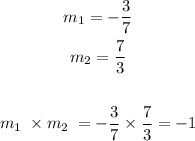
Since the product of their slopes = -1, then they are perpendicular