Question

If sinx= 3/7, we're X in quadrant two then find the exact value of the following in the picture

Answer 1

Given:

The ratio is given as,

`\sin x=(3)/(7)`

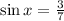
The x is in the second quadrant.

The objective is to find the value of sin2x, cos2x and tan2x.

Step-by-step explanation:

To find cos x :

Using the trigonometric identity,

`\begin{gathered} \sin ^2x+\cos ^2x=1 \\ \cos ^2x=1-\sin ^2x \\ \cos x=\sqrt[]{1-\sin^2x}\text{ . . . . .(1)} \end{gathered}`

On plugging the given values in equation (1),

`\begin{gathered} \cos x=\sqrt[]{1-((3)/(7))^2} \\ =\sqrt[]{1-(9)/(49)} \\ =\sqrt[]{(49-9)/(49)} \\ =\pm\frac{\sqrt[]{40}}{7} \\ =\pm\frac{2\sqrt[]{10}}{7} \end{gathered}`

Since x lies in the second quadrant,

`\cos x=-\frac{2\sqrt[]{10}}{7}`

a)

To find sin(2x):

The general formula to find sin(2x) is,

`\sin 2x=2\sin x\cos x\text{ . . . . .(2)}`

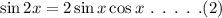
On plugging the obtained values in equation (2),

`\begin{gathered} \sin 2x=2((3)/(7))(-\frac{2\sqrt[]{10}}{7}) \\ =-\frac{12\sqrt[]{10}}{49} \end{gathered}`

Hence, the value of sin(2x) is (-12√10)/49.

b)

To find cos (2x):

The general formula of cos(2x) is,

`\cos (2x)=\cos ^2x-\sin ^2x\text{ . . . . . .(3)}`

On plugging the obtained values in equation (3),

`\begin{gathered} \cos (2x)=(-\frac{2\sqrt[]{10}}{7})^2-((3)/(7))^2 \\ =(4*10)/(49)-(9)/(49) \\ =(40-9)/(49) \\ =(31)/(49) \end{gathered}`

Hence, the value of cos(2x) is 31/49.

c)

To find tan(2x):

The general formula of tan(2x) is,

`\text{tan}(2x)=(\sin2x)/(\cos2x)\text{ . . . . . .(4)}`

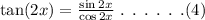
On plugging the obtained values in equation (4),

`\begin{gathered} \text{tan}(2x)=\frac{\frac{-12\sqrt[]{10}}{49}}{(31)/(49)} \\ =-\frac{12\sqrt[]{10}}{31} \end{gathered}`

Hence, the value of tan(2x) is (-12√10/31).