Question

A greeting card company can sell cards for $2.75 each, so the revenue can be calculated using the formula 2.75 Rx . The company’s total cost consists of a fixed overhead of $12,000 plus 35 cents per card, so the total cost can be calculated using the formula 0.35 12000 Cx .

a. Write the algebraic equation needed to determine when the company will break even (when the revenue will equal the cost).

b. Solve the equation from part a.

c. Write the algebraic inequality needed to indicate that the revenue is greater than the cost.

d. Solve the inequality from part c.

e. What does your answer from part d tell you about when the company will make a profit?

Answer 1

Given that the revenue equation is
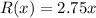
`R(x)=2.75x` and the cost equation is
`C(x)=0.35x+12,000`



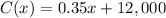
Part A:

At break-even the cost is equal to the revenue.

Thus, the algebraic equation needed to determine when the company will break even is given by


`R(x)=C(x) \\ \\ \Rightarrow2.75x=0.35x+12,000`



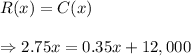
Part B:

The solution to part A is given as follows:


`2.4x=12,000 \\ \\ \Rightarrow x=5,000`



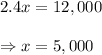
Part C:

The algebraic inequality needed to indicate that the revenue is greater than the cost is given by


`R(x)\ \textgreater \ C(x) \\ \\ \Rightarrow2.75x\ \textgreater \ 0.35x+12,000`



Part D:

The solution to part C is given as follows:


`2.4x>12,000 \\ \\ \Rightarrow x>5,000`



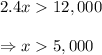
Part E:

The answer in part D tells us that the the company will make a profit when the produce more than 5000 cards.