Question

Which of the following could NOT be the lengths of the sides of a triangle?

A.5 in, 5 in, 5 in
B. 10 cm, 15 cm, 20 cm
C. 3 in, 4 in, 5 in
D. 8 ft, 15 ft, 5 ft

Answer 1

Given:

Sides of triangles in the options.

To find:

Which could NOT be the lengths of the sides of a triangle.

Solution:

Condition for triangle:

Sum of two smaller sides of a triangle must be greater than the longest side.

In option A,

`5+5=10>5`

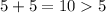
Sides 5 in, 5 in, 5 in are the lengths of the sides of a triangle.

In option B,

`10+15=25>20`

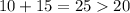
Sides 10 cm, 15 cm, 20 cm are the lengths of the sides of a triangle.

In option C,

`3+4=7>5`

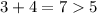
Sides 3 in, 4 in, 5 in are the lengths of the sides of a triangle.

In option D,

`8+5=13<15`

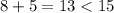
Since, the sum of two smaller sides is less than the longest side, therefore the sides 8 ft, 15 ft, 5 ft are not the lengths of the sides of a triangle.

Therefore, the correct option is D.