Question

What is the domain and range of f(x) = |x + 6|?

domain: (negative infinite,infinite); range: f(x) (greater than or equal to) 0
domain: x (less then or equal to)-6; range: (negative infinite,infinite)
domain: x(greater than or equal to)-6 ; range: (negative infinite,infinite)
domain:(negative infinite,infinite) ; range: f(x) (less than or equal to) 0

Answer 1

x can be any real value so domain is (-INF, INF) . The range can be 0 or greater than zero because it is an absolute function.

The first choice is the correct one.

Answer 2

domain: (negative infinite,infinite); range: f(x) (greater than or equal to
`0`

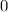
Explanation:

we have

`f\left(x\right)=\left|x+6\right|`

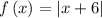
The vertex of the function is the point
`(-6,0)`

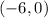
The domain is the interval--------> (-∞,∞)

The domain is all real numbers

The range is the interval ------> [0,∞)

`f(x)\geq 0`

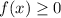
The range is all real numbers greater than or equal to zero

To better understand the problem see the attached figure