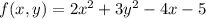
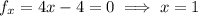
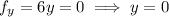
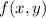
has only one critical point at
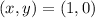
. The function has Hessian
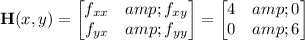
which is positive definite for all
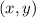
, which means
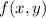
attains a minimum at the critical point with a value of
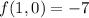
.
To find the extrema (if any) along the boundary, parameterize it by

and
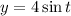
, with
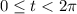
. On the boundary, we have
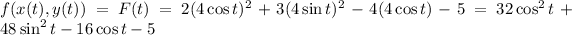

Find the critical points along the boundary:
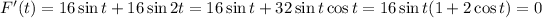
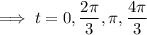
Respectively, plugging these values into
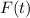
gives 11, 47, 43, and 47. We omit the first and third, as we can see the absolute extrema occur when
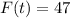
.
Now, solve for
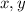
for both cases:
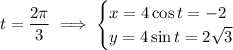

so
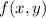
has two absolute maxima at
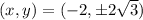
with the same value of 47.