Question

Anthony flipped a coin off his balcony. The function h(t) models the height of the coin (in feet) over timet (in seconds).h(t) = -167 +94 +26Use the model to answer each of the following questions. Round your answers to the nearest thousandth.• What is the height of Anthony's balcony?• What is the maximum height of the coin?After how many seconds does the coin reach its maximum height?• How long does it take for the coin to reach the ground?

Answer 1

To answer this question, we can proceed as follows:

1. We have the function, h(t), that models the height of the coin (in feet) over time t (in seconds) is:

`h(t)=-16t^2+9t+26`

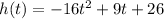
Now we can proceed as follows to answer the questions about the function:

What is the height of Anthony's balcony?

The height of Anthony's balcony can be found at the moment, t = 0, that is, right before Anthony will flip the coin off his balcony, and this represents the y-intercept of this quadratic function. Then we have:

`\begin{gathered} h(0)=-16(0)^2+9(0)+26 \\ h(0)=26 \end{gathered}`

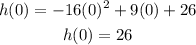
Therefore, Anthony's balcony is 26 feet from the ground.

What is the maximum height of the coin?

After how many seconds does the coin reach its maximum height?

In this case, we can use the formula for the vertex of the parabola, or we can also use the first derivative of the function, and then equates it to zero. We can proceed using the first method:

The coordinates for the vertex of a parabola are given by the next formulas:

`x_v=-(b)/(2a),y_v=c-(b^2)/(4a)`

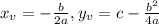
And this is applicable to the general equation:

`ax^2+bx+c`

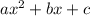
In this case, we have:

`\begin{gathered} -16t^2+9t+26 \\ a=-16,b=9,c=26 \end{gathered}`
`\begin{gathered} x_v=-(b)/(2a) \\ x_v=-(9)/(2(-16))=(9)/(2(16))=(9)/(32)=0.28125 \end{gathered}`

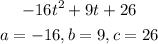
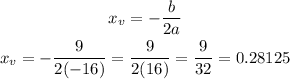
And the coordinate for y (in this case, the maximum height is):

`\begin{gathered} \begin{equation*} y_v=c-(b^2)/(4a) \end{equation*} \\ y_v=26-(9^2)/(4(-16)) \\ y_v=27.265625 \end{gathered}`

Therefore, if we round the results to the nearest thousandth, we have:

The maximum height is (in feet):

`y_v=27.266`

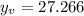
And this height is reached after (in seconds):

`x_v=0.281`

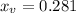
How long does it take for the coin to reach the ground?

To answer this question, we know that when the coin reaches the ground, the height will be h = 0. Then we have to set the equation to zero to find the value for t when the coin reaches the ground:

`\begin{gathered} h(t)=-16t^2+9t+26 \\ 0=-16t^2+9t+26 \\ -16t^2+9t+26=0 \end{gathered}`

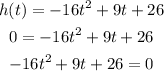
And we can solve this equation using the quadratic formula:

When:

`ax^2+bx+c=0`
`\begin{gathered} a=-16,b=9,c=26 \\ x=(-9+√(9^2-4(-16)(26)))/(2(-16))=(-9+√(1745))/(-32)=-1.02416241089 \\ x=(-9-√(1745))/(-32)=1.58666241089 \\ \end{gathered}`

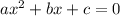
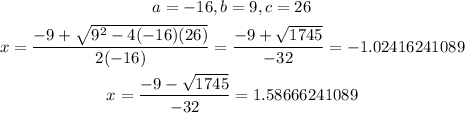
Since the first solution is an extraneous solution, then the solution is (rounded to the nearest thousandth):

`t=1.587`

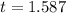
Therefore, the coin will reach the ground at t = 1.587 seconds.

In summary, we have that: