Question

The intelligence quotient (iq) test scores for adults are normally distributed with a mean of 100 and a standard deviation of 15. what is the probability we could select a sample of 50 adults and find that the mean of this sample is between 98 and 103?

Answer 1

The probability that a sample of size n of a normally distributed data with mean, μ and standard deviation, σ, is between two values, a and b, is given by


`P(a\ \textless \ x\ \textless \ b)=P(x\ \textless \ b)-P(x\ \textless \ a) \\ \\ =P\left(z\ \textless \ (b-\mu)/(\sigma/√(n)) \right)-P\left(z\ \textless \ (a-\mu)/(\sigma/√(n)) \right)`

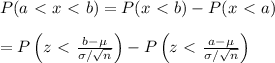
Given that the intelligence quotient (iq) test scores for adults are normally distributed with a mean of 100 and a standard deviation of 15.

The probability that a sample of 50 adults will have a mean of between 98 and 103 is given by:


`P(98\ \textless \ x\ \textless \ 103)=P(x\ \textless \ 103)-P(x\ \textless \ 98) \\ \\ =P\left(z\ \textless \ (103-100)/(15/√(50)) \right)-P\left(z\ \textless \ (98-100)/(15/√(50)) \right) \\ \\ =P\left(z\ \textless \ (3)/(2.121) \right)-P\left(z\ \textless \ (-2)/(2.121) \right) \\ \\ =P(z\ \textless \ 1.414)-P(z\ \textless \ -0.9428) \\ \\ =0.92135-0.17289=0.74846`

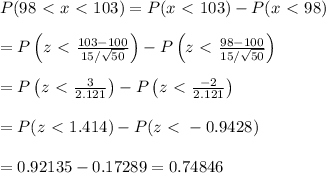
Therefore, the probability that a sample of 50 adults will have a mean of between 98 and 103 is 0.74846