Question

Assume you have such a watch. if a minimum of 18.0% of the original tritium is needed to read the dial in dark places, for how many years could you read the time at night? assume first-order kinetics.

Answer 1

Given that the half life of 3H is 12.3 years.

The amount of substance left of a radioactive substance with half life of
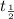
`t_{ (1)/(2) }` after t years is given by


`N(t)=N_0\left((1)/(2) \right)^{ \frac{t}{t_{(1)/(2)} }`

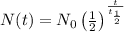
Therefore, the number of years it will take for 18% of the original tritinum to remain is given by


`18 \% = 100 \% \left((1)/(2) \right)^{ (t)/(12.3)} \\ \\ \Rightarrow\left((1)/(2) \right)^{ (t)/(12.3)} =0.18 \\ \\ \Rightarrow(t)/(12.3)\ln\left((1)/(2) \right)=\ln0.18 \\ \\ \Rightarrow(t)/(12.3)= (\ln0.18)/(\ln\left((1)/(2) \right)) = (-1.715)/(-0.6931) =2.474\\ \\ \Rightarrow t=2.474(12.3)=30.4`

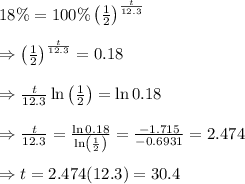
Therefore, the number of years that the time could be read at night is 30.4 years.