Question

Define a new random variable by y = 2px. show that, as p l 0, the mgf of y converges to that of a chi squared random variable with 2r degrees of freedom by showing that

Answer 1

The moment generating function (mgf) of y is given by


`M_y(t)=E(e^(ty))=E(e^(2pxt))=M_x(2pt)=p(1-e^(2pt)(1-p))^(-1)`

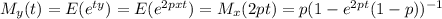
Since the momoent generating function of x is given by
`M_x(t)=p(1-e^(t)(1-p))^(-1)`

When p tends to 0, we have


`\lim_(p \to 0) M_y(t)= \lim_(p \to 0) (p)/(1-e^(2pt)(1-p)) = (0)/(0)`

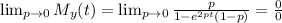
Applying L'Hopital's rule we have:


`\lim_(p \to 0) M_y(t)=\lim_(p \to 0) (1)/(e^(2pt)+2te^(2pt)+2pte^(2pt)) = (1)/(1+2t) , \ \ \ t\ \textless \ (1)/(2)`

This shows that y converges to a chi squared random variable with 2r degrees of freedom.