Question

Verda used a sensor to measure the speed of a moving car at different times. At each time, the sensor measured the speed of the car in both miles per hour and kilometers per hour. The table below shows her results. RECORDED SPEEDS Speed (miles per hour) Speed (kilometers per hour) 17.699 11.0 26.0 41.834 34.0 54.706 If kilometers per hour is represented by x, and miles per hour is represented by y ... A. Does the table show a proportional relationship? EXPLAIN. B. If it shows a proportional relationship, what is the constant of proportionality? C. Write an equation to represent this situation. D. How many miles did a car travel if it went 75 kilometers?

Answer 1

First we have to calculate the rate of change with the first and second pairs of points. And then calculate the rate of change with the second and third pairs. If the slope is the same, data would represent a proportional relationship. The points for calculating the first slope must be ( 17.699, 11) and ( 41.834, 26).

`m=(y2-y1)/(x2-x1)=(26-11)/(41.834-17.699)=0.621`

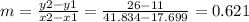
The second slope is going to be calculated with (41.834,26) and (54.706, 34)

`m=(y2-y1)/(x2-x1)=(34-26)/(54.706-41.834)=\text{0}.621`

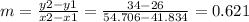
A. Since both slopes have the same value we can deduce this is a proportional relationship.

B. The constant of proportionality must be 0.621

C. The equation that represents that situation must be: Y=0.621*X

D. If a car travels 75 kilometers , then using the equation we obtain

Y=0.621*(75 km/h)=46.575 miles/h