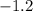The average rate of change is also known as "Slope".
The formula for calculate the slope is the following:
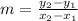
As you can notice, it can be found dividing the change in "y" by the change in "x".
In this case you have the table of a function and you need to find the rate of change over this interval:
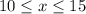
You need to find the corresponding y-values for:
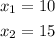
As you can identify in the table, when the value of "x" is:
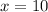
The value of "y" is:
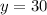
And when
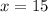
The value of "y" is:
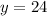
Therefore, you can set up that:
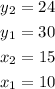
Now you can substitute values into the formula and evaluate:
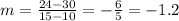
The answers is: