Question

The function H(t) = −16t2 + 48t + 12 shows the height H(t), in feet, of a cannon ball after t seconds. A second cannon ball moves in the air along a path represented by g(t) = 10 + 15.2t, where g(t) is the height, in feet, of the object from the ground at time t seconds.

Part A: Create a table using integers 0 through 3 for the 2 functions. Between what 2 seconds is the solution to H(t) = g(t) located? How do you know? (6 points)

Part B: Explain what the solution from Part A means in the context of the problem. (4 points)

Answer 1

Part A
t 0 1 2 3
H(t) 12 44 44 42
g(t) 10 25 40 56
Set H(t) = g(t) yields 16t^2 -32t -2 which shows its zeroes or points of intersections are at 0.6 and 2.1 seconds
Part B
H(t) = g(t) intersect at (x,y) points (0.6 secs, 9.1 feet) and (2.1 secs, 42.1 feet)
H(t) is a parabola that opens downward which shows the cannonball arches upwards then falls downward.
g(t) is a straight linear line which slopes positive upwards and intersects G(t) in two places.

Answer 2

Answer with explanation:

We are given a function H(t) that represents the height of a cannon ball after t seconds as:

`H(t)=-16t^2+48t+12`

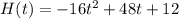
and a second cannon ball is represented by the function g(t) as:

`g(t)=10+15.2t`

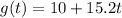
PART A:

t 0 1 2 3

H(t) 12 44 44 12

g(t) 15.2 25.2 40.4 55.6

Hence, between t= 2 seconds and t=3 seconds the ball will meet

such that H(t)=g(t)

Since, we know that the Height H(t) decreases from 44 feet to 12 feet between t=2 to t=3 seconds.

and height g(t) increases from 40.4 feet to 55.6 feet between t=2 to t=3 seconds.

Hence, the two cannon balls will definitely meet between t=2 to t=3 seconds.

and the time at which they meet is calculated by solving:

`H(t)=g(t)\\\\i.e.\\\\\\-16t^2+48t+12=10+15.2t\\\\\\i.e.\\\\\\16t^2-32.8t-2=0\\\\\\i.e.\\\\\\t=-0.059\ and\ t=2.109`

As t can't be negative.

Hence, we get:

t=2.109 seconds

PART B:

The solution from PART A means that the one of the ball first reach the highest point at 44 feet and then returns back to the initial position and hence follows a parabolic path while the second cannon ball reach a greater height with the increase in time and hence in this phenomena the two balls will definitely meet.