Question

Round your answer to this problem to the nearest degree.

In triangle ABC, if ∠A = 120°, a = 8, and b = 3, then ∠B =
°.a0

Answer 1

Use the sine law: sinB/b = sinA/a

SinB = b*sinA/a

sinB = 3*sin120° /8

∠ B = 18.94° ≈ 19°

Answer 2

∠B = 19°

Explanation:

Given : In triangle ABC, if ∠A = 120°, a = 8, and b = 3

We have to find the measure of B that is ∠B

Consider the given triangle ABC,

Using Sine rule ,

For a triangle with measure of angle A, B and C and side a faces angle A,

side b faces angle B and side c faces angle C

`(a)/(\sin A)=(b)/(\sin B)=(c)/(\sin C)`

we have, a = 8 , b = 3 and ∠A = 120°

Consider first two ratios,

`(8)/(\sin 120^(\circ))=(3)/(\sin B)`

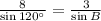
Solve for B, we have,

`\sin \left(120^(\circ \:)\right)=(√(3))/(2)`

`(8)/((√(3))/(2))=(3)/(\sin \left(B\right))`

`\mathrm{Apply\:fraction\:cross\:multiply:\:if\:}(a)/(b)=(c)/(d)\mathrm{\:then\:}a\cdot \:d=b\cdot \:c`

`8\sin \left(B\right)=(√(3))/(2)\cdot \:3`

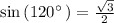
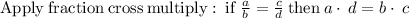
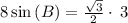
Simplify, we have,

`\sin \left(B\right)=(3√(3))/(16)`

Taking sine inverse both side, we have,

`B=\sin^(-1)\left((3√(3))/(16)\right)`

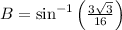
We have,
`B=18.95^(\circ \:)`

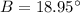
Thus, ∠B = 19°