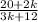Answer:
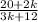
Explanation:
Since there is no equals sign here, we are not solving this. The only way to simplify is to get a common denominator and write the expression as a single expression. We can begin by noting that the second term has a k in the numerator and in the denominator, and those cancel each other out. That is the first simplification we can perform. That leaves us with:
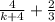
In the first term, the denominator is k + 4, in the second term it is just 3. Therefore, the common denominator is 3(k+4). We are missing the 3 in the denominator of the first term, so we will multiply in 3/3 by that term. We are missing a (k + 4) in the second term, so we will multiply in (k + 4)/(k + 4) by that term:
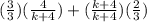
Multiplying fractions requires that I multiply straight across the top and straight across the bottom. That gives me:

Now that the denominators are the same, I can put everything on top of that single denominator:
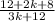
Th final simplification requires that I combine like terms: