Answer:
1 - 2n > 5. The solution set is (-∞, -2)
Explanation:
We are dealing here with two problems:
- First, to determine which mathematical statement represents "One less than twice a number is no less than five".
- Second, solve n, that is, the solution set for the numbers that solve the inequality.
First Part: Identifying the inequality
"One less than twice a number" can be written as
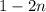 , where n is the unknown number.
, where n is the unknown number.
If it is not less than five, thus it is greater (no less) than five. Then, the symbol here is " > " (greater).
As a result: "One less than twice a number is no less than five" could be rewritten as "One less than twice a number is greater than five", or:
 .
.
Second Part: Finding the solution set
The solution set for this inequality is as follows:
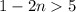 ⇒
⇒
Subtract -1 from each member of the inequality:
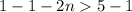 ⇒
⇒
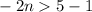 ⇒
⇒
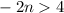
Multiply each member of the inequality by
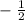 (or divide each member by -2). We have to remember here that when we multiply or divide an inequality by a negative number (-n), this inverts the inequality, that is:
(or divide each member by -2). We have to remember here that when we multiply or divide an inequality by a negative number (-n), this inverts the inequality, that is:


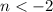
The solution set is then
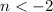 , which is any value less than -2 (not including -2, because is < and not ≤), and we have infinite negative numbers with such a characteristic. We can write it mathematically as an interval notation:
, which is any value less than -2 (not including -2, because is < and not ≤), and we have infinite negative numbers with such a characteristic. We can write it mathematically as an interval notation:
Solution set for
 is
is
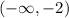 .
.