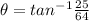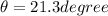Question

While driving north at 25 m/s during a rainstorm you notice that the rain makes an angle of 38° with the vertical. while driving back home moments later at the same speed but in the opposite direction, you see that the rain is falling straight down. from these observations, determine the speed and angle of the raindrops relative to the ground?

Answer 1

`v = 68.7 m/s`

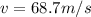
angle made with the vertical

`\theta = 21.3 degree`

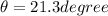
Step-by-step explanation:

Velocity of rain with respect to the car with vertical direction makes 38 degree angle

so let say rain velocity is

`v_r = v_x\hat i + v_y \hat j`

`v_(rc) = v_r - v_c`

`v_(rc) = (v_x + 25)\hat i + v_y`

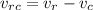
now we have

`tan38 = (v_x + 25)/(v_y)`

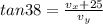
while return to home

`v_(rc) = (v_x - 25)\hat i + v_y`

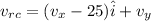
now the angle with vertical is zero

so we have

`v_x = 25`

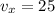
now we have

`tan38 = (50)/(v_y)`

`v_y = 64 m/s`

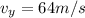
so we have

`v_r = 25 \hat i + 64 \hat j`

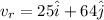
now magnitude of the speed is

`v = √(25^2 + 64^2)`

`v = 68.7 m/s`

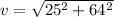
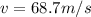
angle made with the vertical

`\theta = tan^(-1)(25)/(64)`

`\theta = 21.3 degree`