Question

Draw the graph of the inequality: y>4x+3 Part a: Find two points on the associated line. Often it's smart to start with the values x = 0 and x = 1.The point (0, ? ) is on the line y=4x+3 .The point (1, ? ) is on the line y=4x+3 .Part b: Find a point that satisfies the strict inequality y>4x+3 .The point (0, ? ) satisfies y>4x+3 .

Answer 1

Step-by-step explanation

In this problem, we have the inequality:

`y>4x+3.`

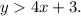
Graph

To plot the inequality, we paint all the points that lie in the region strictly over the line y = 4x + 3:

Part a

To find two points associated with the line, we replace the values x = 0 and x = 1 in the equation:

`y=4x+3.`

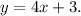
We get the points:

`\begin{gathered} (x,y)=(0,4\cdot0+3)=(0,3), \\ (x,y)=(1,4\cdot1+3)=(1,7). \end{gathered}`

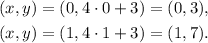
Part b

From the graph above, we see that the point (0, 6) is in the region that satisfies the inequality.

Replacing the coordinates of the point in the inequality, we see that:

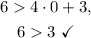
`\begin{gathered} 6>4\cdot0+3, \\ 6>3\text{ \checkmark} \end{gathered}`Answer

Part a

• The point ,(0, 3), is on the line y = 4x + 3.

,

• The point ,(1, 7), is on the line y = 4x + 3.

Part b

• The point ,(0, 6), satisfies y > 4x + 3.