Question

I have a practice question that I need the explanation and answer for. Thank you!What is the distance, d, between the points (2, 5/2) and (8/3, 1)? Enter the answer in simplest radical form.-Rose

Answer 1

Given the points

`\begin{gathered} (x_1,y_1)\Rightarrow(2,(5)/(2)) \\ (x_2,y_2)\Rightarrow((8)/(3),1) \end{gathered}`

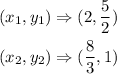
To find the distance, d, between the two points,

The formula is

`d=\sqrt[]{(x_2-x_1)^2+(y_2-y_1)^2}`

Substitute the values into the formula of the distance between two points above

`\begin{gathered} d=\sqrt[]{(x_2-x_1)^2+(y_2-y_1)^2} \\ d=\sqrt[]{((8)/(3)-2)^2+(1-(5)/(2))^2} \end{gathered}`

Solve to find d,

`\begin{gathered} d=\sqrt[]{((8)/(3)-2)^2+(1-(5)/(2))^2} \\ d=\sqrt[]{((2)/(3))^2+(-(3)/(2))^2} \\ d=\sqrt[]{(4)/(9)+(9)/(4)} \\ d=\sqrt[]{(97)/(36)}=\frac{\sqrt[]{97}}{6} \\ d=\frac{\sqrt[]{97}}{6}=1.64\text{ (two decimal places)} \\ d=1.64\text{ (two decimal places)} \end{gathered}`

Hence, the simplest radical form of the distance, d, between the two given points is 1.64 ( two decimal places).