Question

Calculus: Help ASAP

Evaluate exactly the value of the integral from negative 1 to 0 of the product of the cube of the quantity 4 times x to the 6th power plus 2 times x and 12 times x to the 5th power plus 1, dx. Your work must include the use of substitution and the antiderivative.

Answer 1

`\bf \displaystyle \int\limits_(-1)^(0)~(4x^6+2x)^3(12x^5+1)\cdot dx\\\\ -------------------------------\\\\ u=4x^6+2x\implies \cfrac{du}{dx}=24x^5+2\implies \cfrac{du}{2(12x^5+1)}=dx\\\\ -------------------------------\\\\ \displaystyle \int\limits_(-1)^(0)~u^3\underline{(12x^5+1)}\cdot\cfrac{du}{2\underline{(12x^5+1)}}\implies \cfrac{1}{2}\int\limits_(-1)^(0)~u^3\cdot du\\\\ -------------------------------\\\\`


`\bf \textit{now, we'll change the bounds, using u(x)} \\\\\\ u(-1)=4(-1)^6+2(-1)\implies u(-1)=2 \\\\\\ u(0)=4(0)^6+2()\implies u(0)=0\\\\ -------------------------------\\\\ \displaystyle \cfrac{1}{2}\int\limits_(2)^(0)~u^3\cdot du\implies \left. \cfrac{1}{2}\cdot \cfrac{u^4}{4} \right]_(2)^(0)\implies \left. \cfrac{u^4}{8} \right]_(2)^(0)\implies [0]-[2]\implies -2`

Answer 2

2.264 (3 d.p.)

Explanation:

Given integral:

`\displaystyle \int^0_(-1) \left(4x^6+2x\right)^3\left(12x^5+1\right)\;\text{d}x`

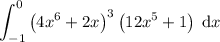
First, evaluate the indefinite integral using the method of substitution.

`\textsf{Let} \;\;u = 4x^6+2x`

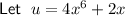
Find du/dx and rewrite it so that dx is on its own:

`\frac{\text{d}u}{\text{d}x}=24x^5+2 \implies \text{d}x=(1)/(24x^5+2)\; \text{d}u`

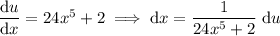
Rewrite the original integral in terms of u and du, and evaluate:

`\begin{aligned}\displaystyle \int\left(4x^6+2x\right)^3\left(12x^5+1\right)\;\text{d}x&=\int \left(u\right)^3\left(12x^5+1\right)\cdot (1)/(24x^5+2)\; \text{d}u\\\\&=\int \left(u\right)^3\left(12x^5+1\right)\cdot (1)/(2(12x^5+1))\; \text{d}u\\\\&=\int (u^3\left(12x^5+1\right))/(2(12x^5+1))\; \text{d}u\\\\&=\displaystyle \int (u^3)/(2)\; \text{d}u\\\\&=(u^(3+1))/(2(3+1))+C\\\\&=(u^4)/(8)+C\end{aligned}`

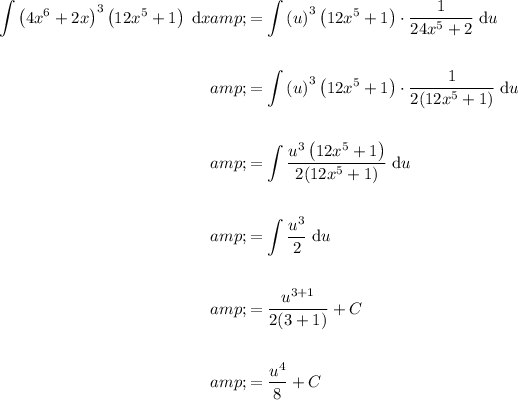
Substitute back u = 4x⁶ + 2x:

`=((4x^6+2x)^4)/(8)+C`

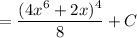
Therefore:

`\displaystyle \int \left(4x^6+2x\right)^3\left(12x^5+1\right)\;\text{d}x=((4x^6+2x)^4)/(8)+C`

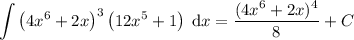
To evaluate the definite integral, we must first determine any intervals within the given interval -1 ≤ x ≤ 0 where the curve lies below the x-axis. This is because when we integrate a function that lies below the x-axis, it will give a negative area value.

Find the x-intercepts by setting the function to zero and solving for x.

`\left(4x^6+2x\right)^3\left(12x^5+1\right)=0`

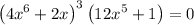
Therefore:

`\begin{aligned}\left(4x^6+2x\right)^3&=0\\4x^6+2x&=0\\x(4x^5+2)&=0\end{aligned}`

`x=0`

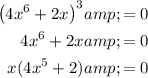
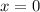
`\begin{aligned}4x^5+2&=0\\4x^5&=-2\\x^5&=-(1)/(2)\\x&=\sqrt[5]{-(1)/(2)}\end{aligned}`

`\begin{aligned}12x^5+1&=0\\12x^5&=-1\\x^5&=-(1)/(12)\\x&=\sqrt[5]{-(1)/(12)}\end{aligned}`

Therefore, the curve of the function is:

• Below the x-axis between -1 and ⁵√(-1/2).
• Above the x-axis between ⁵√(-1/2) and ⁵√(-1/12).
• Below the x-axis between ⁵√(-1/12) and 0.

So to calculate the total area, we need to calculate the positive and negative areas separately and then add them together, remembering that if you integrate a function to find an area that lies below the x-axis, it will give a negative value.

Integrate the function between -1 and ⁵√(-1/2).

As the area is below the x-axis, we need to negate the integral so that the resulting area is positive:

`\begin{aligned}A_1&=-\displaystyle \int_(-1)^{\sqrt[5]{-(1)/(2)}} \left(4x^6+2x\right)^3\left(12x^5+1\right)\;\text{d}x\\\\&=-\left[((4x^6+2x)^4)/(8)\right]_(-1)^{\sqrt[5]{-(1)/(2)}}\\\\&=-\left[\left(\frac{\left(4\left(\sqrt[5]{-(1)/(2)}\right)^6+2\left(\sqrt[5]{-(1)/(2)}\right)\right)^4}{8}\right)-\left(((4(-1)^6+2(-1))^4)/(8)\right)\right]\\\\&=-[0-2]\\\\&=2\end{aligned}`

Integrate the function between ⁵√(-1/2) and ⁵√(-1/12).

`\begin{aligned}A_2&=\displaystyle \int_{\sqrt[5]{-(1)/(2)}} ^{\sqrt[5]{-(1)/(12)}} \left(4x^6+2x\right)^3\left(12x^5+1\right)\;\text{d}x\\\\&=\left[((4x^6+2x)^4)/(8)\right]_{\sqrt[5]{-(1)/(2)}}^{\sqrt[5]{-(1)/(12)}}\\\\&=\left(\frac{\left(4\left(\sqrt[5]{-(1)/(12)}\right)^6+2\left(\sqrt[5]{-(1)/(12)}\right)\right)^4}{8}\right)-\left(\frac{\left(4\left(\sqrt[5]{-(1)/(2)}\right)^6+2\left(\sqrt[5]{-(1)/(2)}\right)\right)^4}{8}\right)\\\\\end{aligned}`

`\begin{aligned}&=\frac{625}{648\sqrt[5]{12^4}}-0\\\\&=0.132117398...\end{aligned}`

Integrate the function between ⁵√(-1/12) and 0.

As the area is below the x-axis, we need to negate the integral so that the resulting area is positive:

`\begin{aligned}A_3&=-\displaystyle \int_{\sqrt[5]{-(1)/(12)}}^0 \left(4x^6+2x\right)^3\left(12x^5+1\right)\;\text{d}x\\\\&=-\left[((4x^6+2x)^4)/(8)\right]_{\sqrt[5]{-(1)/(12)}}^0\\\\&=-\left[\left(((4(0)^6+2(0))^4)/(8)\right)-\left(\frac{\left(4\left(\sqrt[5]{-(1)/(12)}\right)^6+2\left(\sqrt[5]{-(1)/(12)}\right)\right)^4}{8}\right)\right]\\\\&=-\left[0-\frac{625}{648\sqrt[5]{12^4}}\right]\\\\&=\frac{625}{648\sqrt[5]{12^4}}\\\\&=0.132117398...\\\\\end{aligned}`

To evaluate the definite integral, sum A₁, A₂ and A₃:

`\begin{aligned}\displaystyle \int^0_(-1) \left(4x^6+2x\right)^3\left(12x^5+1\right)\;\text{d}x&=2+2\left( \frac{625}{648\sqrt[5]{12^4}}\right)\\\\&=2+ \frac{625}{324\sqrt[5]{12^4}}\right}\\\\&=2.264\; \sf (3\;d.p.)\end{aligned}`