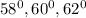Solution:
Given:
The angles of a triangle are as shown in the sketch below;
Consecutive even integers are the set of integers such that each integer in the set differs from the previous integer by a difference of 2 and each integer is divisible by 2.
For the three angles to be consecutive even integers, then

Since the three angles are in the triangle, then;
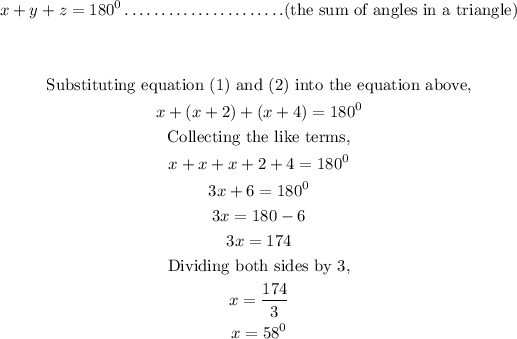
Substituting the value of x into equations (1) and (2) to get the values of y and z,
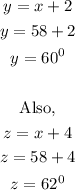
Therefore, the measure of each angle if the angles are consecutive even integers are;