Answer:
A combination of 9 bills and 5 coins is the least number of bills and coins.
Explanation:
A customer has six (6) $1 bills, three (3) $5 bills, four (4) $10 bills, seven (7) quarters, ten (10) dimes, seven (7) nickels, and nine (9) pennies.
1 quarter = $0.25
1 dime = $0.10
1 penny = $0.01
1 nickel = $0.05
The customer buys a pair of shoes for $49.86.
So, we can split this as following:
49 can be split as 40+9
So,
 bills =$40
bills =$40
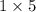 bill = $5
bill = $5
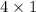 bill = $4
bill = $4
Total is $49 made from 9 bills.
For the decimal part, we can split as :
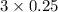 quarters = $0.75
quarters = $0.75
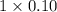 dime = $0.10
dime = $0.10
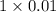 penny = $0.01
penny = $0.01
Total becomes = $0.86 from 5 coins.
Hence, a combination of 9 bills and 5 coins is the least number of bills and coins the customer can give the cashier in order to buy the shoes for the exact amount and not require any change back.