Question

1) Write the sum or difference in the standard form a + bi. (2 points)

( 7 + 5i) - ( -9 + i)

a) 16+4i
b) -16-4i
c) 16-4i
d) -2+6i

2) Write the product in standard form. (2 points)
( 7 + 7i)( 6 + 7i)

a) -7 + 91i
b) 49i2 + 91i + 42
c) 91 - 7i
d) -7 - 91i

3) Find the product of the complex number and its conjugate. (2 points)
1 + 3i

a) 1 + 9i
b) 10
c) -8
d) 1-9i

4) Write the expression in standard form. (2 points)
three divided by quantity three minus twelve i.

a) - one divided by seventeen. + four divided by seventeen. i
b) one divided by seventeen. - four divided by seventeen. i
c) - one divided by seventeen. - four divided by seventeen. i
d) one divided by seventeen. + four divided by seventeen. i

5) Find the real numbers x and y that make the equation true. (2 points)
5 + yi = x + 3i

Answer 1

When performing addition and multiplication with constant numbers, we treat i as we would treat any variable x in an expression, with the same rules and properties of addition and multiplication.

1)


`( 7 + 5i) - ( -9 + i)=7+5i+9-i=(7+9)+(5i-i)=16+4i`

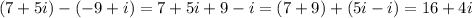
2)
Distribute 7+7i over 6 and 7i:


`( 7 + 7i)( 6 + 7i)=( 7 + 7i)\cdot6+( 7 + 7i)\cdot7i=42+42i+49i+49i^2`

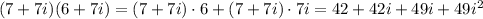
collecting similar terms, and substituting
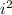
`i^2` with -1 we have:

42+91i-49=-7+91 i

3)

The conjugate of a complex number a+bi is a-bi;
the conjugate of 1+3i is 1-3i.

Thus, using the difference of squares formula we have


`(1+3i)(1-3i)=1^2-(3i)^2=1-9i^2=1-9(-1)=1+9=10`

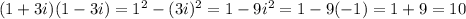
4)

To write a rational expression ( with a complex number in the denominator) in the standard form, we multiply by the conjugate of the denominator both the numerator and the denominator:


`\displaystyle{ (3)/(3-12i)= (3(3+12i))/((3-12i)(3+12i))= (9+36i)/(3^2-(12i)^2)`


`=\displaystyle{ (9+36i)/(9+144)= (9+36i)/(153)= (9)/(153)+ (36)/(153)i`


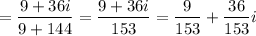
simplifying by 9, the complex number is finally written as


`\displaystyle{ (1)/(17)+ (4)/(17)i`


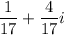
5)

2 complex numbers a+bi, and c+di are equal only if a=c, and b=d. (Where a, b, c, d are real numbers.)

Thus, x=5, and y=3 is the solution to the equation.


Answers:

1) A
2) A
3) B
4) D
5) (x, y) =( 5, 3)