It helps to first clarify that the notation (f - g)(x) simply means f(x) - g(x). Given that, let's look at our f(x) and our g(x) here, and use their definitions to find their difference.
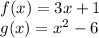
When we're taking (f - g)(x), we simply substitute the expression 3x + 1 for f(x) and the expression x² - 6 for g(x) to obtain:
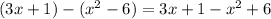
Or, ordering the polynomial from highest power to lowest and combining the constants:

Edit: By request, here's what would happen if you had something instead like:
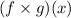
In this case, you'd have to *multiply* the two function expressions together. Here's what that would look like:
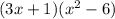
Using the distributive property, we can distribute the expression

to the terms
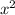
and
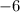
:
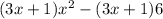
Distributing again, we get:

And we're done.