Question

Find all exact solutions on the interval [0, 2pi). cos(8×) + cos(4x) = 0x=

Answer 1

To solve the equation we must change cos(8x) to cos(4x) using the expression of double angles

cos(8x) = 2cos^2(4x) - 1

2cos^2(4x) - 1 + cos(4x) = 0

Arrange the terms

`2\cos ^2(4x)+\cos (4x)-1=0`

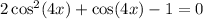
Now let us factorize it into two brackets

(2cos(4x) - 1)(cos(4x) + 1) = 0

Now equate each bracket by 0

cos(4x) + 1 = 0

cos(4x) = -1

The value of cos = -1, when 4x = pi

You must find the domain of 4x

The domain of x is [0, 2pi]

The domain 4x is [0, 8pi]

So you have 4 cycles of the angle

So you must add 2pi for the angle in each cycle then divide the angle by 4

4x = pi, 4x = 3pi , 4x = 5pi, 4x = 7pi

Divide all by 4

x = pi/4, 3pi/4, 5pi/4, 7pi/4

Now let us do the same with the 2nd bracket

2cos(4x) - 1 = 0

2cos(4x) = 1

cos(4x) = 0.5

Cos is positive in 1st and 4th quadrants

The angle which has cos = 0.5 is pi/3

So 4x = pi/3 or 2pi - pi/3 = 5pi/3

Add for each one 2pi as we did with the first value 4 times

4x = pi/3, pi/3 + 2pi, pi/3 + 4pi, pi/3 + 6pi,

4x = pi/3, 7pi/3, 13pi/3, 19pi/3

Divide all by 4

x = pi/12, 7pi/12, 13pi/12, 19pi/12

The solution for 5pi/3

4x = 5pi/3, 5pi/3 + 2pi, 5pi/3 + 4pi, 5pi/3 + 6pi

4x = 5pi/3, 11pi/3, 17pi/3, 23pi/3

Divide all by 4

x = 5pi/12, 11pi/12, 17pi/12, 23pi/12

`x=(\pi)/(4),\frac{3\text{ }\pi}{4},\frac{5\text{ }\pi}{4},(7\pi)/(4)`

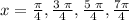
This answer for the first bracket

`x=(\pi)/(12),\frac{7\text{ }\pi}{12},\frac{13\text{ }\pi}{12},\frac{19\text{ }\pi}{12}`

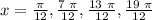
This answer for the 1st angle in the 2nd bracket

`x=\frac{5\text{ }\pi}{12},\frac{11\text{ }\pi}{12},\frac{17\text{ }\pi}{12},\frac{23\text{ }\pi}{12}`

This answer for the second angle in the 2nd bracket