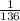Question

A local pizza parlor has the following list of toppings available for selection. the parlor is running a special to encourage patrons to try new combinations of toppings. they list all possible two topping pizzas ( 2 distinct toppings) on individual cards and give away a free pizza every hour to a lucky winner. Find the probability that the first winner randomly selects the card for the pizza topped with red peppers and green olives. express your answer as a fraction pizza toppings: green peppers, onions, kalamata olives, sausage, mushrooms, black olives, pepperoni, spicy italian sausage, roma tomatoes, green olives, ham, grilled chicken, jalapeño peppers, banana peppers, beef, chicken fingers and red peppers

Answer 1

Find the probability that the first winner randomly selects the card for the pizza topped with red peppers and green olives.

We must first find all the possibilities for the two topping pizzas ( 2 distinct toppings) that corresponds to the number if cards.

When choosing any topping we have 17 options and after that for the second topping we have 16 options

`17\cdot16=272`

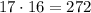
Here we repeat each option twice because it appears for example (green peppers, onions) and (onions,green peppers) , to eliminate the ones that we repeat, we divide by 2.

`(272)/(2)=136`

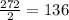
This corresponds to the combination of 17 combined by 2, 136 possibilities.

Then, the probability that the first winner randomly selects the card for the pizza topped with red peppers and green olives is:

`(1)/(136)`