Question

Alex had (3x + 1) yards of silk. He then purchases (x2 + 5x + 4) packages each containing (2x + 1) yards of silk. If he uses (2x3 + 8x2 + 10x + 4) yards of silk to make a kite, how much silk remains?

Answer 1

Alex has originally
`3x+1` yards of silk.

Then he purchases
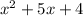
`x^2+5x+4` packages, each containing
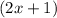
`(2x+1)` yards of silk, so he purchases a total of


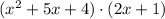
`(x^2+5x+4)\cdot(2x+1)` yards of silk.

Distributing
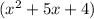
`(x^2+5x+4)` over
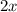
`2x`, and 1 we have


`(x^2+5x+4)\cdot2x+(x^2+5x+4)\cdot+1=2x^3+10x^2+8x+x^2+5x+4`


`=2x^3+11x^2+13x+4`.


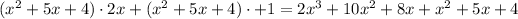
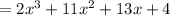
The original amount of silk, and the purchased amount are a total of


`=2x^3+11x^2+13x+4 + (3x+1)=2x^3+11x^2+16x+5`.


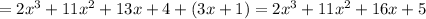
Of these,
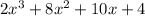
`2x^3+8x^2+10x+4` are used. Thus, in the end the amount left is

`available\ amount-used\ amount`:



`(x^3+11x^2+16x+5)-(2x^3+8x^2+10x+4)=-x^3+3x^2+6x+1`


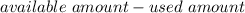
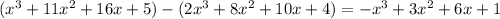
Answer:
`-x^3+3x^2+6x+1` yards