Question

Trigonometric area formula: Area = 1/2 ab sin(c)

What is the area of triangle DEF? Round to the nearest tenth of a square unit.

10.3 square units
18.0 square units
20.0 square units
20.6 square units

Answer 1

10.3= the awnser

Explanation:

just took test and got it right.

Answer 2

1. 10.3 square units.

Step-by-step explanation:

The general formula for area of triangle is
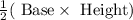`(1)/(2)(\text{ Base}*\text{ Height}})`. We can also find area of a triangle using trigonometric area formula.

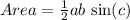`Area=(1)/(2) ab\text{ sin}(c)`, where a represents length of base and height of triangle is represented by
`b\text { sin}(c)`.

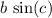We have been given two angle measures but we can only use sine of included angle whose two side lengths are given. In our triangle the angle that measures 31 degrees in included angle of sides EF and DF.

Now let us substitute our given values in the above formula.

`Area=(1)/(2)* 8* 5\text{ sin}(31)`

`Area=(1)/(2)* 8* 5* 0.51503807491`

`Area=4* 5 * 0.51503807491`

`Area=20 * 0.51503807491`

`Area=10.3007614982\approx 10.3`

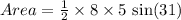
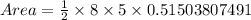
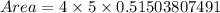
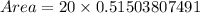
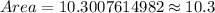
Therefore, the area of triangle DEF is 10.3 square units and 1st option is the correct choice.