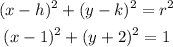From the statement of the problem we know the following facts about a circle:
- its center is at the point:
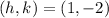
- it's tangent to the y-axis.
Using the data above we draw the following graph of the circle:
From the graph, we see that the circle center is at a distance of 1 unit from the y-axis (to which it is tangent), so the circle has a radius:
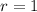
Replacing the data of the center and the radius in the general form equation of the circle, we get: