If we follow that two quantities are proportional, they need to be multiplied by a factor. If they are directly proportional, the value is a factor that multiplies the relationship. If they are inversely proportional, the value is a reciprocal factor that multiplies this relationship. This factor must be the same for the relationship.
Then, we have that the only factor is:
x y
-1 1
-3 3
-5 5
Since we have that
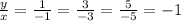
The factor is constant, it is the same for all the values. Then, this table, the second one, represents a proportional relationship (the second option):
x y
-1 1
-3 3
-5 5
The other tables represent different relationships or proportions between the variables (following the same procedure):
The first option has different values for the relationship of y/x = (-1, -1/2, -1/5), the third has (5/2, 7/4, 3/2), and the last one (0, 1/3, 1/2). The second table gives us a unique value for the relationship between the variables y/x = (-1, -1, -1).